丰巢安卓版

“万能代换”通常指的是一种在数学或物理问题中使用的技巧，它允许你用一个表达式或变量来代替另一个表达式或变量，以简化问题或求解过程。这种技巧在代数、微积分、概率论等领域都有广泛应用。
例如，在微积分中，你可能会使用代换法来求解一个积分问题。代换法的基本思想是，通过找到一个合适的代换，将原积分转化为一个更容易计算的形式。这个代换通常涉及到将积分变量替换为一个新变量，同时调整积分的上下限和被积函数。
在概率论中，代换法也可以用来简化随机变量的分布函数或密度函数的计算。通过找到一个合适的代换，可以将随机变量的分布函数或密度函数转化为一个更容易处理的形式。
代换法的关键在于找到一个合适的代换，这个代换应该能够简化问题或求解过程。在实际应用中，代换的选择可能需要一些经验和技巧。但是，一旦找到了合适的代换，它就可以大大简化问题的求解过程，提高求解效率。
请注意，以上解释仅针对“万能代换”在数学和物理问题中的应用。在不同的领域或情境下，“万能代换”可能有不同的含义或应用方式。

万能代换在数学中的应用与技巧

在数学学习中，万能代换是一种重要的解题方法，尤其在处理三角函数、有理式积分等问题时，能够简化计算过程，提高解题效率。本文将详细介绍万能代换的概念、应用场景以及解题技巧。

一、什么是万能代换

万能代换，顾名思义，是一种通用的代换方法。在数学中，当遇到某些复杂函数或表达式时，可以通过引入新的变量，将原函数或表达式转化为更简单、易于处理的形式。这种代换方法被称为万能代换。

二、万能代换的应用场景

1. 三角函数问题：在处理三角函数的求值、证明、化简等问题时，万能代换可以简化计算过程，提高解题效率。

2. 有理式积分问题：在求解有理式积分时，万能代换可以将被积函数转化为更简单的形式，便于计算。

3. 高等数学问题：在处理一些高等数学问题，如级数求和、微分方程等，万能代换也是一种有效的解题方法。

三、万能代换的解题技巧

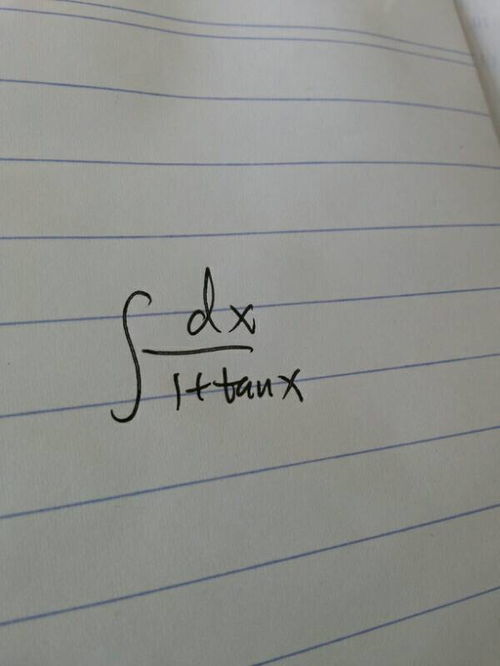
1. 选择合适的代换变量：在进行万能代换时，首先要选择合适的代换变量。一般来说，代换变量应满足以下条件：

（1）代换变量与原变量之间存在简单的函数关系；

（2）代换变量在原函数或表达式中出现频率较高；

（3）代换变量在计算过程中易于处理。

2. 确定代换公式：根据所选代换变量，确定相应的代换公式。常见的代换公式有：

（1）万能三角代换：sinx = t，cosx = √(1-t^2)；

（2）万能有理式代换：x = √(a^2-t^2)，其中a为常数。

3. 代换后的计算：将原函数或表达式中的变量替换为代换变量，然后进行相应的计算。在计算过程中，要注意以下事项：

（1）代换后的表达式应尽量简化；

（2）计算过程中，要注意符号的运用；

（3）在最后一步，要将代换变量还原为原变量。

四、万能代换的实例分析

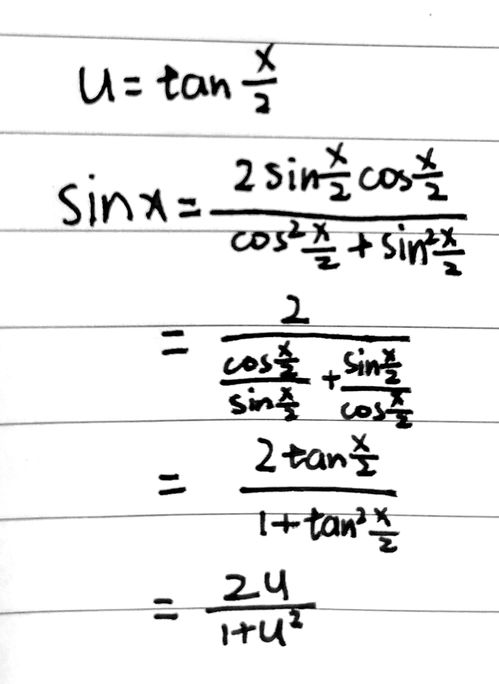
1. 三角函数问题：求sin(2x) cos(2x)的值。

解：令t = tan(x/2)，则sin(2x) cos(2x) = (2t)/(1 t^2) (1-t^2)/(1 t^2) = 1。

2. 有理式积分问题：求∫(x^2)/(1 x^4)dx。

解：令x = √(a^2-t^2)，则dx = -a/t^2dt，原式可转化为∫(a^2-t^2)/(1 a^2t^2)dt。通过万能代换，可得到∫(1-t^2)/(1 t^2)dt，进一步计算得到结果。

万能代换是一种有效的数学解题方法，在处理三角函数、有理式积分等问题时，能够简化计算过程，提高解题效率。掌握万能代换的概念、应用场景以及解题技巧，对于提高数学解题能力具有重要意义。